Last week we had to hustle to keep the cherry blossom mob happy:
Now, imagine that in an alternate universe, the D.C. government decided (questionably) to build a floating walking path straight across the middle of the basin. The idea was to help with pedestrian traffic flow — even if it meant ruining some of the scenic views 😅.
While the path was being constructed, the parks department needed to fence it off to keep curious visitors from using it too soon. So they decided to throw up a temporary barrier somewhere across the basin. The only rule? It had to cut across the floating path to block it. Beyond that, they didn’t overthink it—they just picked two random spots along the shoreline and stretched a rope between them.
Now that construction is done, you — a humble parks worker — are on your way to remove the barrier and finally open the path to the public. But halfway there, you realize…you forgot the map! The map would’ve told you which of the two ends of the floating path the barrier is closer to, so you could have picked the shorter walk.
You’re not sure if it’s worth turning back, so instead you ask:
What’s the expected ratio of the shorter segment of the path to the longer one, given that the barrier randomly intersects the path?
Thanks to
and Vamshi Jandhyala for your solutions! I pretty sure the answer was 1/3 but this one was tricky.The first step in the problem was recognizing that in order for a chord to intersect the diameter of the circle, it had to have one point on the upper half of the circle and another point on the lower half. As long as it satisfied those conditions, the points could be placed randomly anywhere in their respective halves. Let’s model our circle as having radius 1, and be centered at the origin. Our diameter will be along the x-axis.
From here, we can set up some linear equations to derive an expression for the x-intercept of the chord.
After some algebra and trig identities, we can get to
Recall that we want the ratio of the smaller portion of the intersected diameter over the larger section of the intersected diameter. This can be written as
Now we could stop here and numerically evaluate the following integral
But let’s see if we can transform this expression into something that can be solved analytically. First, we will transform the variables
To perform this change we’ll need to compute the determinant of the Jacobian and analyze the new limits of integration. Omitting the gritty details, we get that
By symmetry, we can concern ourselves only with a single quadrant of the diamond. With that we can rewrite the integral as
This was as far as I could get analytically with this. To be honest, everything else I tried from here failed. Nevertheless, I’m reasonably confident that the answer is 1/3. If we numerically evaluate the first integral expression from above, we get 1/3 and a Monte Carlo simulation of the problem verifies this answer. A little underwhelming, I know :/
If you managed to evaluate that integral analytically, please post in the comments! I’d love to see how it’s done. As always, please comment with any thoughts or feedback you had on this problem or if you approached it differently. Thanks for reading!



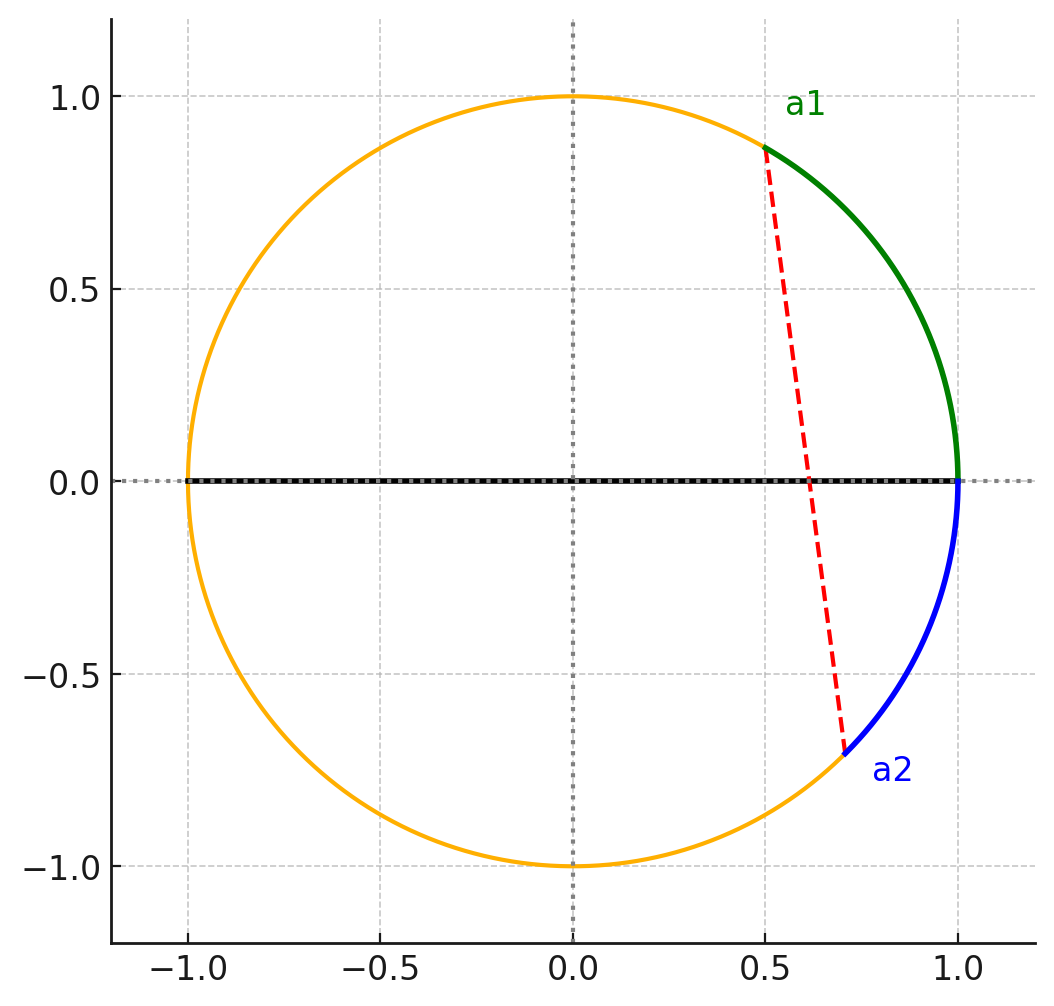
I thought I had an analytic solution but realized it was wrong after I posted the problem. My apologies!
Yes I was just thinking about how the answer was similar! I’m going to go back and look into that a little. I’ll post a note and update the post if I find anything.
Ah... so I wasn't the only one that couldn't get the integral to work :)
Given how close it was to the chord paradox results I figured I had missed a trick or something