Our puzzle last week had us figuring out how to protect our inherited Truffula forest.
You and your three siblings are at the reading of the will for your late father—a wealthy outdoorsman—that owned a forest of very rare and valuable trees known as Truffula trees. The Truffula forest has a single clear center, and from that center outward, the density of trees drops by 50% for every kilometer you travel outward.
In his will, your father decides to split the forest evenly between you and your three siblings by creating 4 equal quadrants emanating from the center of the forest
Each sibling has very different intentions for their forest so you all agree to the creation of a fence that will section off each sibling’s quadrant. For your quadrant, you also want to make to keep the Truffula trees protected so you decide to create a fence around the outside of your quadrant (something like a circumference). To minimize fencing costs, you plan to stretch the fence snugly around just the trees at the forest’s outer edge, keeping all other trees safely within the boundary (see the red line). To actually build this fence, you'll need special posts every time the fence changes direction around these outermost trees. You also find that your section of the forest has 1000 trees.
The question for this week is, on average, how many fence posts will you need?
Thanks to solvers
and Vamshi for your submissions. Some readers may have recognized this problem as a relatively well known problem in algorithms—computing the convex hull over a set of point. A convex hull refers to the convex polygon drawn over a set of points such that it covers all of them with minimum area.Those that attempted this problem may also have found it rather messy mathematically. That’s because I made a mistake. I meant for the problem to be a bit easier but in translating the intended problem into a “story” format, I accidentally introduced a gnarly complexity. The problem was originally supposed to have the x-coordinate and y-coordinate be independent so we could make some simpler arguments about how the set of Pareto dominant points converges on the number of points in the outer hull as the number of trees gets large. But the tree description I provided with it’s radial symmetry most certainly doest not have x-y independence. Honestly, a similar argument might be workable but it’s much less obvious to me.
Being that this mistake caught me a bit off guard, I didn’t have as much time to work on a solution as I would have liked. I came up with the solution below but the answer it yields is different to what my simulations suggest, indicating the solution is probably wrong. In fact, solver
’s solution get’s closer to the simulated values I found and he’s a sharp fellow so his solution is much more likely the correct one. I present my solution as well just in case it spurs any thoughts or if anyone can spot an error (which likely exists).The Best Answer We Have…
Check out Izumihara’s solution here.
My [Probably Wrong] Solution…
How do we construct the convex hull? For the most part, we just need one reasonably simple observation. A line is part of the convex hull if all the points we are trying to cover lie on one side of the line. In the case we’re consider where all the points are in the upper right quadrant, this simplifies to all the points being “less” than a line on the outer hull. Let’s say point A and B make up this line. They have coordinates rA, θA, rB, and θB . The line they form is given by
Also, before we progress much further, we should describe the distribution of trees in the quadrant
There are n-2 points that remain that need to be less than the line r(θ). The probability of any one of these points being greater than the line is
As such, the probability of all of the points be less than line AB is
Now recall that
is a conditional probability. So we’ll need to compute the marginal with respect to A and B.
We also need to consider that fact that there are (n choose 2) possible choices for A and B. Putting this together we get
Where Hn is the number of vertices in the outer hull. That leaves us with this monstrosity.
Now there are some simplifications we can make to this expression but I don’t this even yields the correct answer so I won’t bother here. The computational evaluation of this integral gives 4.8031 fence posts. This is a bit high compared to Izumihara’s 3.02 solution and my own simulation results which yielded 2.82 (turns out even simulating this problem isn’t super straightforward 😕)
In any case, I’ve run out of time for this writeup. Apologies to my readers for the mistake. I’m a little embarrassed about this snafu and will try to be more careful moving forward. I hope to see you for the next puzzle!

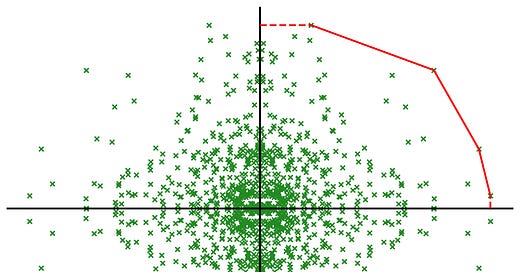


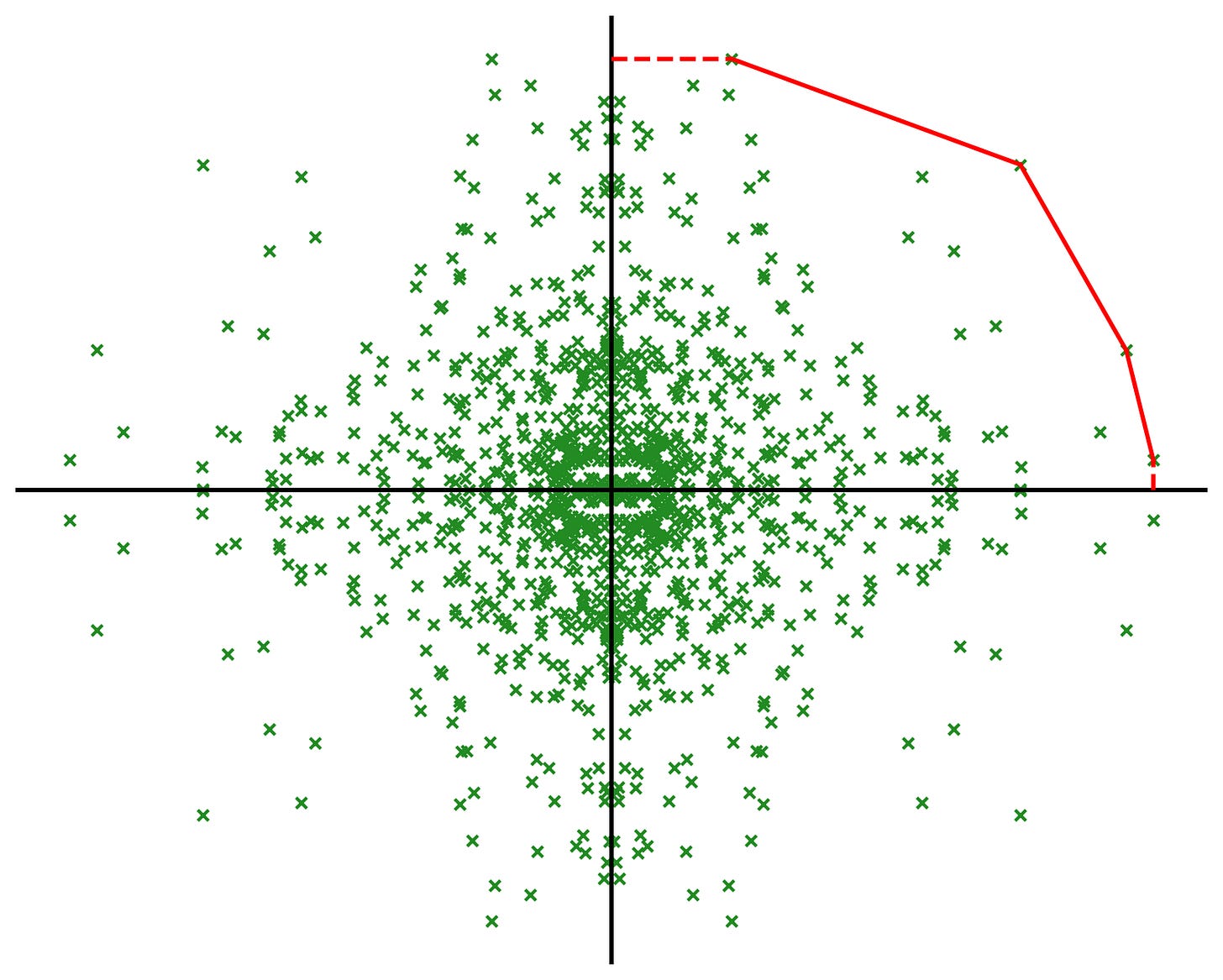
I simulated this one extensively. The expected number of posts is slightly more than 3, somewhere between 3.01 and 3.02.
The first time I tried to calculate the answer to the puzzle I was using a spreadsheet to simulate the forest and find the number of points in the convex hull (for that model I figured out which points were extreme points in different discrete directions, like each integer degree angle, which is almost always the same as the actual convex hull) the expectation came out to 3.14..., which had me thinking the result might just be pi. It is not.
I tried to find some way to express the number of posts as a function of angle (including the stated condition that when the angle is close to 360° the two bounding fences are still there). The relationship is almost, but not quite, linear.
(For those who are interested, you can generate the locations of the trees by producing polar coordinates where the radius has a probability density function f(r)=r*ln(0.5)*exp(r*ln(0.5)), and cumulative distribution F(r)=1+exp(r*ln(0.5))*(r*ln(0.5)-1). The angle is uniformly distributed from 0 to 90°, which can be changed to any range up to 360°. Producing a random variable with a given distribution can be done by getting a random probability, uniformly distributed from 0 to 1, and then taking the inverse CDF, which in this case must be done numerically.)
As was often the case with your puzzles, I ended up having a lot of fun exploring the problem, but didn't produce any results that were mature enough to justify writing up. Alas.
Thank you for sharing such an interesting problem and for including my solution.
I do have one question regarding your simulation.
In your simulation, did you sample the variable r from an exponential distribution with λ equal to log(2) (that is, using a probability density given by 0.5^r × log(2)) and select θ uniformly from the interval [0, π/2] to determine the locations of 1000 trees?
If that is the case, then the model does not actually reflect the scenario described in the problem, where the tree density halves every kilometer.
In general, using the same probability density for r as for the x-y coordinates does not necessarily yield the intended distribution.
For instance, if you sample 1000 values of r uniformly from [0, 1] and 1000 values of θ uniformly from [0, 2π], and then plot the points, you will likely notice that the distribution of points is not uniform.
To illustrate this effect, consider running the following Python code:
import numpy as np
import matplotlib.pyplot as plt
r = np.random.uniform(0, 1, 1000)
theta = np.random.uniform(0, 2*np.pi, 1000)
x = r * np.cos(theta)
y = r * np.sin(theta)
plt.scatter(x, y, marker=".")
plt.axis("equal")
plt.show()
In this example, the average number of points between r = 0.1 and r = 0.1 + Δr is the same as between r = 0.9 and r = 0.9 + Δr.
However, because the area corresponding to the outer region around r = 0.9 is approximately nine times larger than that at r = 0.1, the density in the outer region ends up being about one-ninth of that in the inner region.
The same effect occurs in the probability distribution for this problem, so directly using the x-y density as the probability density for r does not achieve the desired outcome.