Ocean's 4 [solution]

Solution for the week of 6/8

Last week we found ourselves scheming against our fickle friend:

The game starts with an empty unit circle. Players place a point in the circle one at a time (player 1 first, player 2 second, etc.) until each player has gone. After everyone has selected, a random point is sampled uniformly from the unit circle. The player whose point is closest to the randomly sampled point is the winner.

Your friends decide to take the egalitarian approach and give each player an equal probability of winning. To accomplish this you all decide to select the center of one of the circle’s quadrants (think center of mass).

This is the strategy the friends planned on employing.

The first three players go and they each select a quadrant center. The last player—whom you’ve never fully trusted—decides to be greedy and select the point that maximizes his odds of winning. What point does he select and what are his odds of winning?

You and your two friends that just got duped are rather mad. The croupier managing the game offers for you all to play again on the condition that you retain the same order you played the first time. You all accept (it is after all free money at the end of the day) but the three of you decide you are going to conspire against the 4th player this time. The three of you need to figure out how to place your points such that player 4’s chances of winning are minimized.

Shout out to solvers Peter Ji of Madison, WI (hey, are you a fellow Badger?) and Izumihara Ryoma of Japan. The both got this week’s puzzle correct!

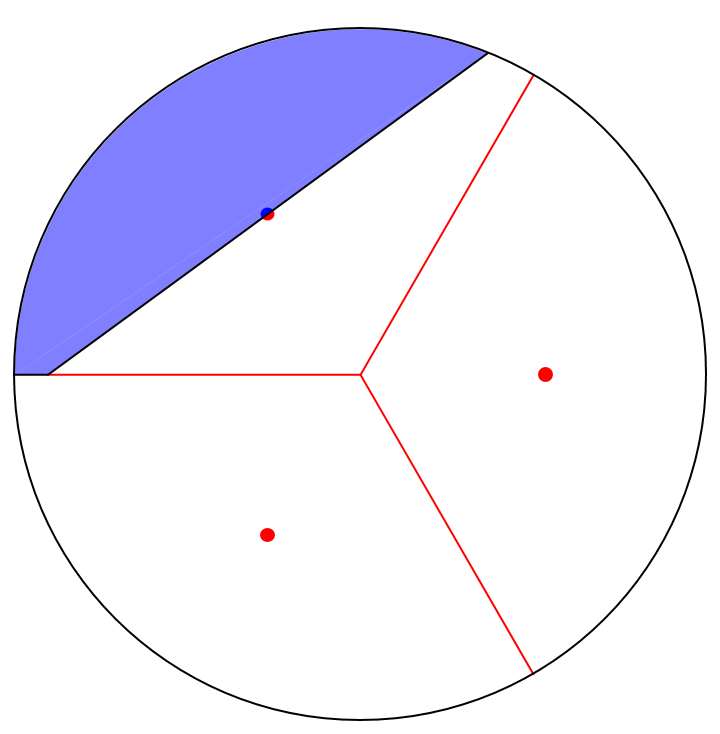
So if you’re player 4, what’s the best way to betray your friends? To start, we need to consider how the placement of the point influences your probability of winning. To do this we will use what’s called a Voronoi diagram. A Voronoi diagram separates our playing space into regions where each region is ‘controlled’ by one of the players. In more mathematical terms, for any one of the player’s selected point, there is a set of points in the unit circle which are closest to that point than any other. The collection of all of these points creates a Voronoi cell. This concept is important because the space ‘controlled’ by a particular player basically gives us the probability they will win the game. So if we can compute the size of each player’s Voronoi cell, we will have everything we need to solve the problem.

Ok, but we still need to decide on a point before we can create a Voronoi diagram. Any position we may choose is parameterized by the distance from the origin r and the angular position on the circle. In this case, determining the angle is pretty intuitive; the optimal orientation is on player 4’s quadrant bisector.

We can construct an argument that shows that, regardless of where you are along the bisector, it’s always worse to move away from it, but I image most folks can intuitively see that this is correct.

So now we’re left with the question of where along the bisector to place our point. I’m not going to go over all of the details (it gets long and tedious) but we’ll cover a few of the key concepts that are needed. First though, we’ll note that the centroid of a quarter sector is

\(x = y = \pm \frac{4}{3 \pi}\)

There’s a fun derivation of this expression using the expression for the centroid of a circular arc wire which you can find here.

Now, in order to compute a player’s claimed area on the board, we first need to find a way to compute the boundaries between different players’ regions. To do this we will note the the boundary occurs at the set of points P for which

\(\Vert P - P_1 \Vert^2 = \Vert P - P_2 \Vert^2\)

If we let P₁ have coordinates (x₁, y₁) and P₂ have (x₂, y₂) then we end up with an equation like

\((x_2 - x_1)x + (y_2 -y_1)y = \frac{x_2^2-x_1^2 + y_2^2-y_1^2}{2}\)

We can construct such an equation for each pair P₄-P₁, P₄-P₂, and P₄-P₃ and each will be needed at some point. If r_Pi is the distance P_i is away from the origin, then Player 4’s Voronoi cell will have a triangular shape (except that one of the sides is curvilinear) when r_P4 > r_P1 and will have a quadrilateral shape (again, with the exception of one side which is curvilinear) when r_P4 < r_P1.

And with these two facts, we pretty much have everything we need. After much algebra, geometric wrangling, and a change of variables where u is the line x=y, we end up with the following horrifying expression

\(\begin{align*} &A(r) = \frac{1}{d}\Bigl[ \bigl(d^{2}-r^{2}\bigr)\bigl(u_\star-u_{0}\bigr) + r\bigl(u_\star^{2}-u_{0}^{2}\bigr) \Bigr] \;+\; \frac{\pi}{2} \;-\; u_\star\sqrt{1-u_\star^{2}} \;-\; \arcsin u_\star \\ & \qquad d \;=\; \frac{4\sqrt{2}}{3\pi}, \\ & \qquad u_{0}(r) \;=\; -\frac{d^{2}-r^{2}}{2\bigl(d+r\bigr)}, \\ &\qquad u_\star(r) \text{ is the relevant root of } \bigl(2ur - r^{2} + d^{2}\bigr)^{2} \;=\; 4d^{2}(1-u^{2}). \end{align*}\)

We would then differentiate this equation and set it to zero to find its maximum which ends up being at the point (.188, -.188) and giving Player 4 a 28.7% chance of winning. Wow, less than a 4% increase in your chances. That’s not much.

The Voronoi cell for Player 4 when playing optimally. Image is curtesy of Peter Ji

Of course, the easier way to solve this problem is definitely with the help of a computer. With help from packages like shapely, one can (relatively) easily code up the game board and iterate to find the optimal placement.

---

For the second part, I won’t be presenting an analytic method because I didn’t even attempt one (and I’m not sure any of the other solvers did either). As best I can tell, everyone did this one computationally.

Now here is where things get a little speculative. I’m not totally sure that the geometry I’m about to describe is optimal. After reading Peter and Izumihara’s solution, I get the sense that all of us assumed that the optimal defensive configuration for the first three players was in an equilateral triangle. I couldn’t find any way to prove that this is the best configuration and my more general computational attempts (think simulated annealing over a discretized circle) to find an optimal defensive strategy didn’t quite yield an equilateral triangle but seemed to converge on similar-ish configurations. So all said and done, I’m not totally sure this is correct but all of us solvers seem to think this is the best answer :)

As mentioned, I assumed that the first three players select an equilateral triangle for their defensive position and that Player 4’s best move is somewhere ‘inbetween’ two of these points (see the blue dotted line in the image).

The question then just becomes (1) what is the optimal size of the equilateral triangle and (2) exactly where should player 4 play along the dotted line?

In my sweep for the best solution, I found that the first three players should form a triangle with radius of about .435 and player 4 picks a point .437 away from the center. this gives a win percentage of 16.7% (curiously its almost exactly 1/6). Solvers Peter and Izumihara got similar but slightly different answers. I’m guessing the differences between our answers were probably due some discretizing of the circle in order to perform our parameter sweeps.

The Voronoi cell for the Player 4 when the first 3 players coordinate their moves against 4. Image curtesy of Izumihara.

Interestingly, Izumihara also found another solution that doesn’t conform to the solution geometry described above.

Izumihara’s alternate solution that yields the same probability of winning for Player 4.

A plot that justifies why I think my answer is most accurate but honestly, there may be some subtle inaccuracy with my solution so who knows ¯\_(ツ)_/¯

So in this case, Player 4’s decision to betray their friends was definitely a mistake. Anyway, I hope folks had fun thinking about this problem. Till next time!

---

By the way, I haven’t been able to find a solution in the literature for computing optimal play for an N-player, 2D, sequential, Voronoi game. I was a little surprised. Let me know if you’re aware of any such solution. If not, maybe this a good candidate for someone to take a stab at an unsolved problem 👀