Inspired by the Fiddler on the Proof (formerly The Riddler), X’s Puzzle Corner aims to produce a weekly puzzle for readers that enjoy math, probability, and algorithms. Please submit your solution! Solutions will be accepted until 11 pm the following Sunday after the puzzle is posted (in this case 10/20/24). While it isn’t required, I encourage you to opt to have your solution shared so that we all get the chance to see how others thought about and attempted the problem!
The answers of all those that volunteered their solutions will be posted around Wednesday at 10 am.
In many cases, I expect the readers will be better puzzlers than me so I make no guarantees the solutions are correct. I also make no promises about having worked out the solutions to the puzzles ahead of time so it may be the case that they’re very challenging. Part of the fun is finding out!
This weeks puzzle will explore rolling some…Platonic origami!
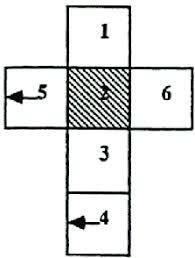
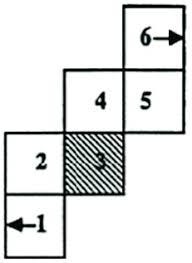
You and your friends are trying to play monopoly but you realize the game is missing a set of dice. You have some monopoly money on hand so you decide you will make the dice by cutting out some paper and taping the necessary side together to make a cube. To make the construction of the cube simpler, you decide you will cut out a single piece of paper. As you’re tracing the shape you’re about to cut out, you realize there are a number of different configurations of the 6 faces you could choose so that, when folded properly, make a cube.
Here’s one possible configuration.
Here’s another:
You start wondering how many different possibilities there are.
So the questions for this week are:
How many unique 2D shapes can be created if we ‘unfold’ the faces of the cube into one continuous piece.
How many for a dodecahedron?
An icosahedron?
For those that are interested, I had been trying to work on a Part 4 for the Get Rich or Buy Trying series but I didn’t quite like how the problem came out. I’ll leave it here for any ambitious problem solvers.
Now that you answered Warren’s questions, he finally gives you your prize. Turns out he was exaggerating a bit and only had one daily oracle. Before you have a chance to protest the violated conditions of the agreement (those last few problems weren’t easy!) he disappeared. Still, you’re happy you have the opportunity to use this daily oracle. You’d like to get a better understanding of its value so you pose the following problem to yourself.
Assume the oracle will tell you wither a stock will go up 1% or down 1% over the day. The stock will move up or down each hour according to a Brownian Bridge process. you start with p_0=1 and can either buy or sell the stock (no short selling). What your expected returns if you trade optimally intra-day for 7 hours as a function of the variance of the stock movement? In the case of the brownian bridge, the variance would be: