Running from Samsquanch - Part 2
Puzzle for the week of 9/8/24
Inspired by the Fiddler on the Proof (formerly The Riddler), X’s Puzzle Corner aims to produce a weekly puzzle for readers that enjoy math, probability, and algorithms. Please submit your solution! Solutions will be accepted until 11 pm the following Sunday after the puzzle is posted (in this case 9/15/24). While it isn’t required, I encourage you to opt to have your solution shared so that we all get the chance to see how other’s thought about and attempted the problem!
The answers of all those that volunteered their solutions will be posted Wednesday at 10 am.
In many cases, I expect the readers will be better puzzlers than me so I make no guarantees the solutions are correct. I also make no promises about having worked out the solutions to the puzzles ahead of time so it may be the case that they’re very challenging. Part of the fun is finding out!
Last week we were were introduced to a hairy dilemma…
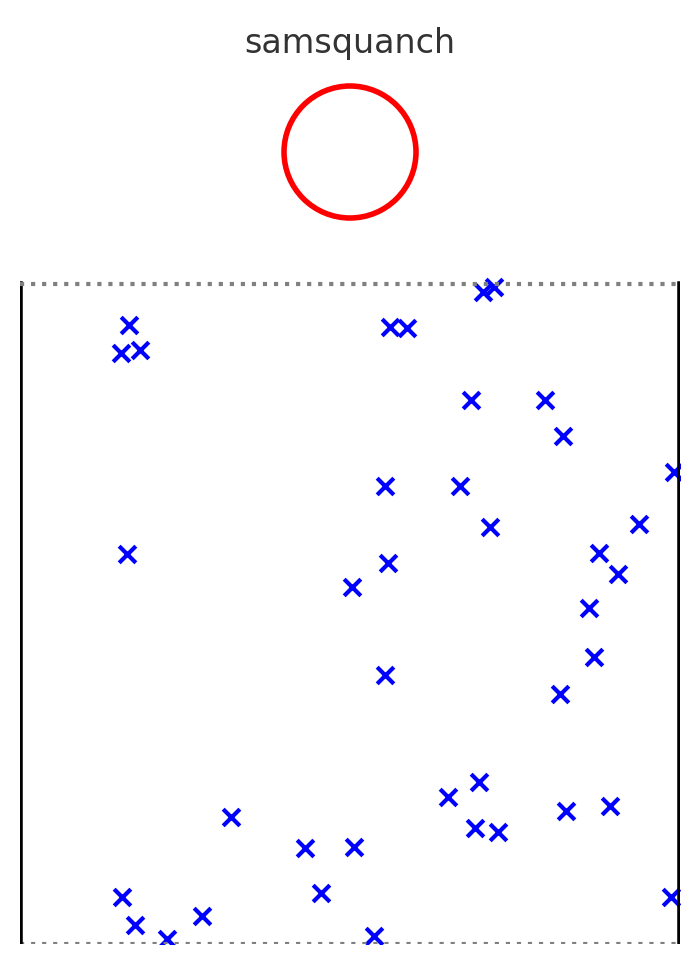
You’re thinking about doing a backpacking trip through Rainier National Park but there’s one big concern; that’s Samsquanch territory! After thinking it over for a moment you realize you have one big advantage; Samsquanch’s broad shoulders make it more difficult to navigate dense trees while your small, nerdy frame can fit quite easily. In order to make sure you have a chance to escape, you want to make sure the forest you’re hiking through has sufficient tree density.
Let’s model our forest as a 10x10 square. The top will be the entrance and the bottom will be the exit. For simplicity, we will assume the sides are impassable barriers. Each tree will be modeled by a point and Samsquanch will be modeled by a circle of radius 1. Trees will be distributed uniformly in the 10x10 square. Let’s further assume that Samsquanch can’t fit between any two trees that are less than 2R apart. We need to figure out what density the trees need to be in order for you to evade Samsquanch.
Here’s a visualization.
This week, we will do another related but simpler problem (a warmup if you will). Instead of navigating through a 2D forest, Image you just have to determine if Samsquanch can fit through a particular line of trees. The trees are uniformly distributed on a line of length 10. In other words, you need to identify if there are any gaps in this line of length at least 2. Assume there are 7 trees on this line. What is the probability that Samsquanch can fit through this barrier of trees?
Please submit your answers here.