Story left to the reader as an exercise [solution]

Solution for the week of 4/20

Recall our puzzle from 4/20 was

You start with a regular triangle. At the midpoint of each side you draw a circle on the inside of the triangle where the circle is tangent to the side. Each circle is the same size and its radius is maximized such that the interior circles touch each other. Below is a diagram to illustrate.

If we consider a regular triangle, what is the ratio of the area of the 3 interior circles to the area of the triangle? How about a square? How about a regular N-gon?

Congratulations to solver Vamshi Jandhyala for their correct solution! Both the blessing and the curse with geometry problems is that everyone tends to solve them differently, and that was exactly the case this week :)

It seems that this was a problem where once we make a particular observation, the problem becomes nearly trivial. The particular observation can be seen almost immediately if you draw lines from each vertex of an n-gon to the center. it should look something like this.

You’ve probably already noticed that each N circles is perfectly inscribed within the N isosceles triangles formed by adding the lines between vertices and center. From here we can find a general expression for the area of the triangles formed by some N-gon and then find an expression for the circle inscribed in that triangle.

Pardon the informal diagram. I was having a hard time getting ChatGPT to generate a good diagram and I didn’t want to take the time to create it myself 😅

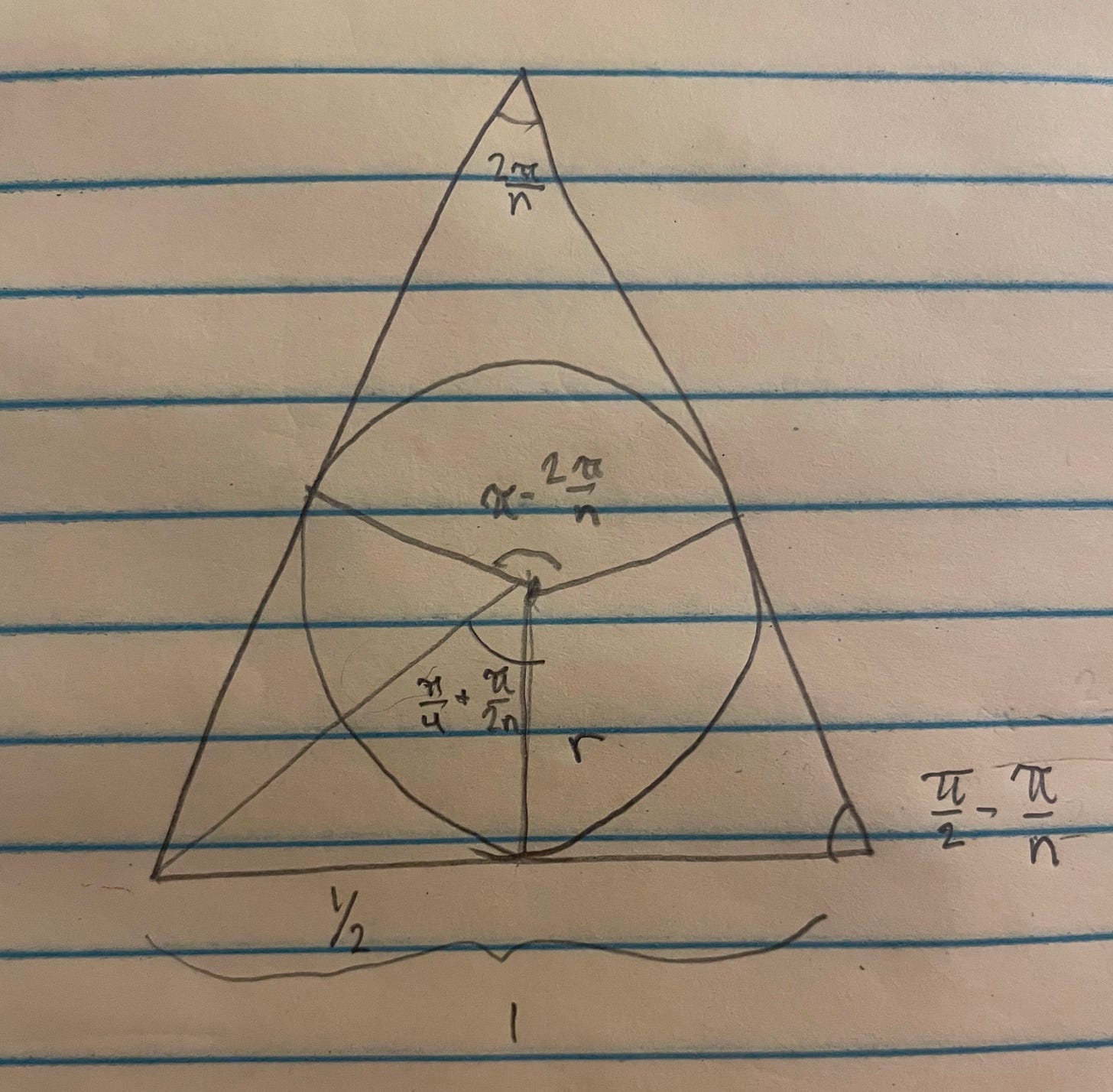
For the triangle, we know the non-shared angle will be 2π/n. For simplicity, I assumed that the sides of any N-gon we consider is s=1. From there we can derive expressions for the height of this triangle and the radius of the inscribed circle.

\(\begin{align*} h &= \frac{\cos(\frac{\pi}{2})}{\sin(\frac{\pi}{n})} \\ r &= \frac{\cos(\frac{\pi}{2})}{2(1+\sin(\frac{\pi}{n}))} \end{align*}\)

Then its as simple as plugging these values into into the well known equations for the area of a triangles and circles. After a little more algebra, we get

\(R = \frac{A_{\text{circles}}}{A_{\text{polygon}}} = \frac{\pi \sin(\frac{2\pi}{n})}{2 (1+\sin(\frac{\pi}{n}))^2}\)

Pluggin in values for n=3 and n=4 we get

\(\begin{align*} n &= 3 \Rightarrow R = \frac{\pi \sqrt{3}}{7+4 \sqrt{3}} \\ n &= 4 \Rightarrow R = \frac{\pi}{3+2 \sqrt{2}} \end{align*}\)

And that’s all there is to it. A pretty simple problem if you find can spot the inscribed circle detail.

As always, please comment with any thoughts or feedback you had on this problem or if have any ideas for extensions of this problem. Thanks for reading!