The Hottest New NYT Game?

Puzzle for the week of 5/11

Inspired by the Fiddler on the Proof (formerly The Riddler), X’s Puzzle Corner aims to produce a weekly puzzle for readers that enjoy math, probability, and algorithms. Please submit your solution! Solutions will be accepted until 11 pm the following Sunday after the puzzle is posted (in this case 5/18/25). While it isn’t required, I encourage you to opt to have your solution shared so that we all get the chance to see how others thought about and attempted the problem! The solution and submitted responses will be posted around Wednesday at 10 am.

I make no guarantees my solutions are correct! You are all smart people so please comment if you think I made a mistake!

---

The next few weeks will feature puzzles intended to set the scene and build into a fascinating result from the recent paper A Hyper-Catalan Series Solution toPolynomial Equations, and the Geode. I was tempted not to mention the paper as the influence but it’s such an interesting result that I couldn’t resist. Just know that reading the paper will result in puzzle spoilers :)

---

You and your friend are playing a variant of the game Dots and Boxes. In this variation, your board is now a regular octagon. You take turns drawing lines between two non-neighboring vertices with the following rules:

1. You can’t cross an existing line

2. If your line creates a triangular face, you get to claim that face and score +1. If you manage to create two triangular faces, you get both of those faces for +2

3. You and your opponent proceed until no more lines can be drawn

At the end, whoever has more points wins.

Below is a simple animation to illustrate

Blue goes first. Red goes second and completes a triangle, which secures that face for red. Blue goes next and completes two triangles, securing both for blue.

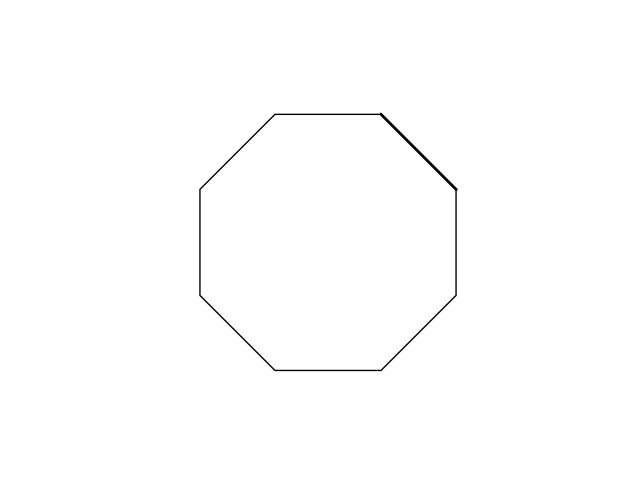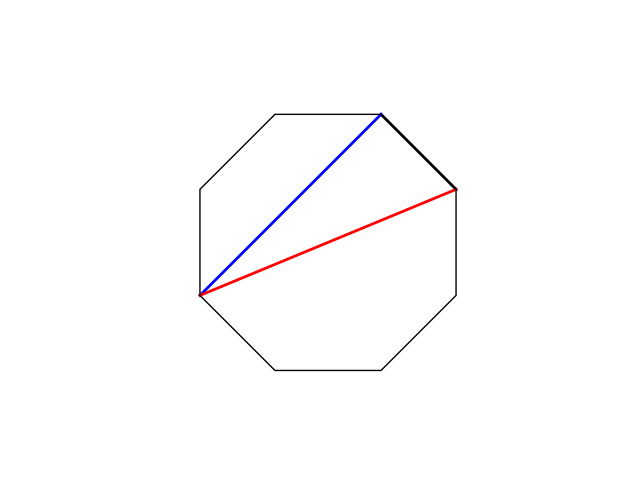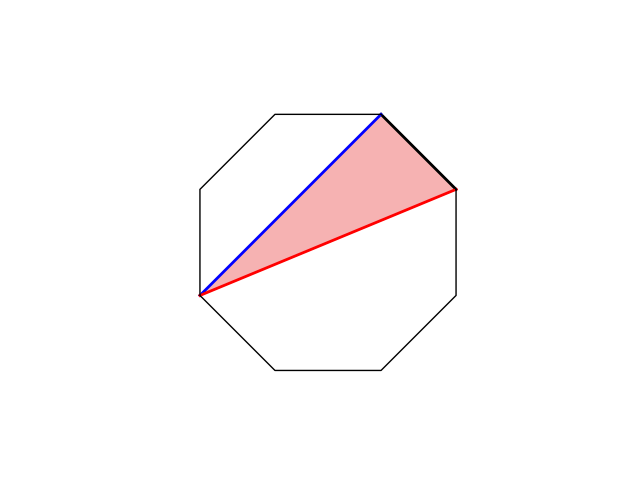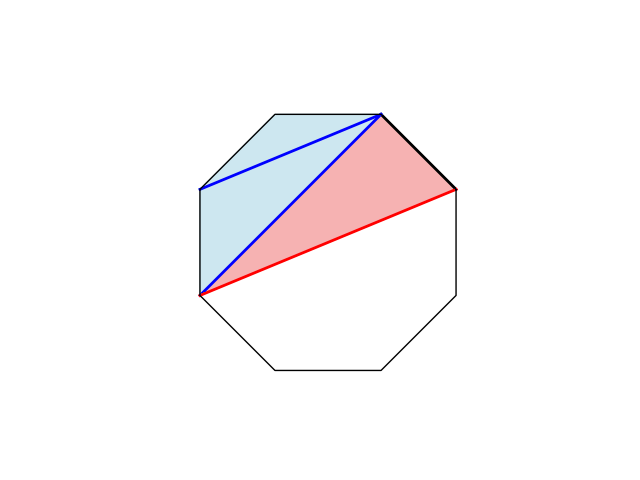
The questions for this week are:

1. If both players play randomly, what’s the probability that Player 1 wins?

2. What is the optimal play for both players?

3. Under optimal play, what is the outcome of the game?

For those courageous solvers, answer each of these questions for a regular n-gon.

Please submit your answers here. Please ask any questions in the comments.