Thinking Inside The Box
Problem for the week of 12/21
Inspired by the Fiddler on the Proof (formerly The Riddler), X’s Puzzle Corner aims to produce puzzles for readers that enjoy math, probability, and algorithms. Please submit your solution! Solutions will be accepted until 11 pm the following Sunday after the puzzle is posted (in this case 12/28/25). While it isn’t required, I encourage you to opt to have your solution shared so that we all get the chance to see how others thought about and attempted the problem! The solution and submitted responses will be posted around Wednesday at 10 am.
I make no guarantees my solutions are correct! You are all smart people so please comment if you think I made a mistake!
It’s late on Christmas Eve, and you’re wrapping presents. As a silly little joke, you like to overwrap your gifts—placing each present inside a box, then inside a larger box, and so on. You head to the basement to grab boxes at random.
Each box is a rectangular prism, and its three side lengths are chosen independently and uniformly at random from the interval [0,1].
First gift. You pick two boxes. What is the probability that one box can fit entirely inside the other?
Second gift. This time you pick three boxes. What is the probability that they can be fully nested—one inside a second, which is itself inside a third?
General case. What is the probability that N randomly chosen boxes can be completely nested?
Correction/Extra Credit
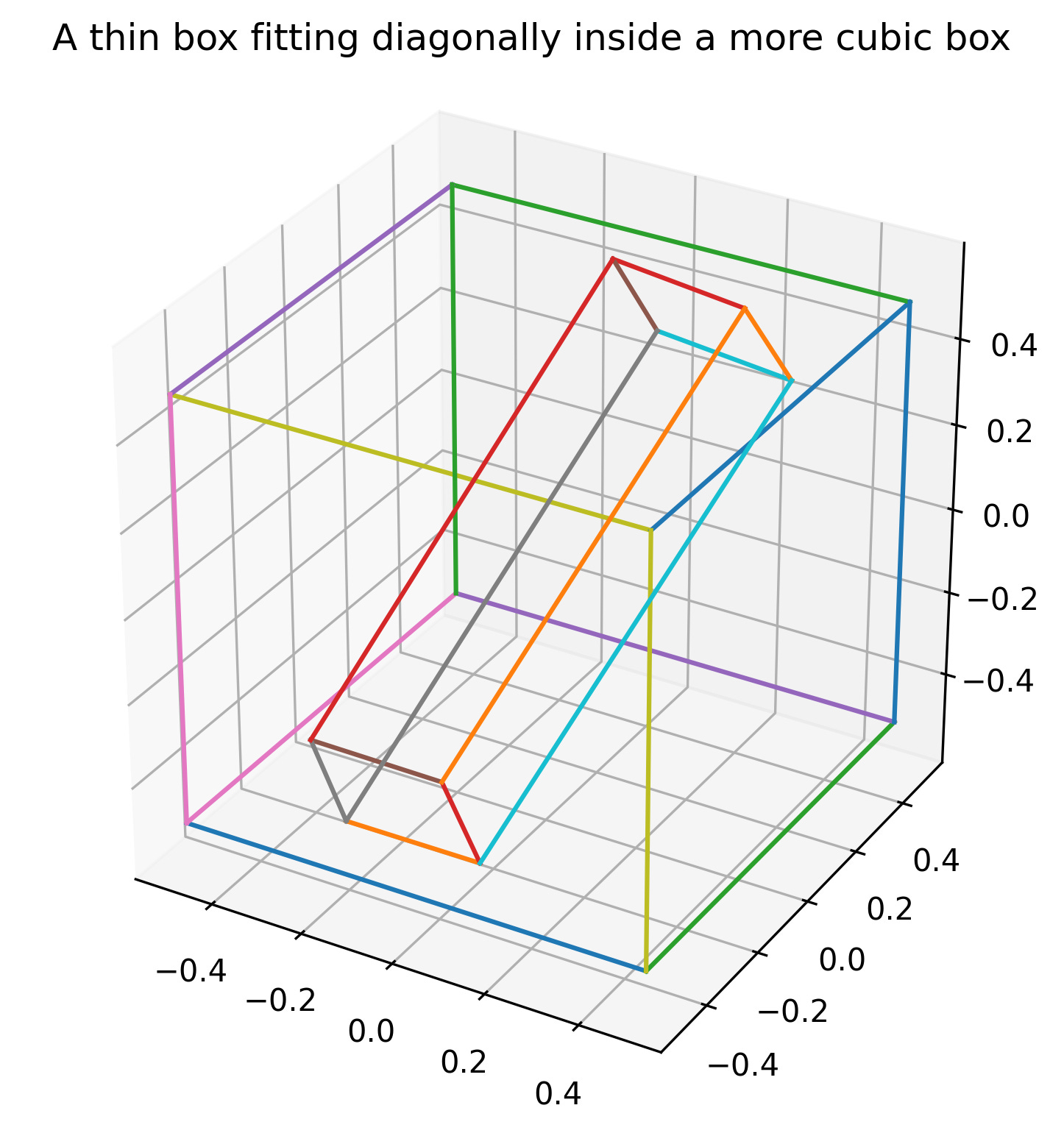
Thanks to David Hobby for his astute observation.
A box need not necessarily fit into another box in an axis aligned way. For example, a relatively ‘thin’ box (two small dimensions and one larger dimension) can be fit into another more more ‘cubic’ box diagonally even if every dimension of the ‘cubic’ box is smaller that the ‘thin’ box’s large dimension.
For the purposes of this puzzle, I was only considering the case where boxes stay axis-aligned. However determining the probabilities when allowing for non-axis-aligned orientations sounds like an interesting and very challenging extra credit problem :)
Please submit your answers here. Please ask any questions in the comments.