Inspired by the Fiddler on the Proof (formerly The Riddler), X’s Puzzle Corner aims to produce a weekly puzzle for readers that enjoy math, probability, and algorithms. Please submit your solution! Solutions will be accepted until 11 pm the following Sunday after the puzzle is posted (in this case 9/29/24). While it isn’t required, I encourage you to opt to have your solution shared so that we all get the chance to see how others thought about and attempted the problem!
The answers of all those that volunteered their solutions will be posted Wednesday at 10 am.
In many cases, I expect the readers will be better puzzlers than me so I make no guarantees the solutions are correct. I also make no promises about having worked out the solutions to the puzzles ahead of time so it may be the case that they’re very challenging. Part of the fun is finding out!
For this weeks puzzle, it’s your birthday! Being such, your 59,049 closest family and friends have come together to get you a rather remarkable gift—a 10-dimensional cake. Think of all the frosting! You’ve made your wish and blown out your candles and, of course, you wished for a good puzzle because you’re a dork. All that’s left is to cut the cake with your handy dandy 10-dimensional knife. In an act of providence, your friend asks “What’s the quickest way to cut this?” and you realize, you have your puzzle you wished for!
More specifically, 59,049 happens to be 310 so to keep things simple you decide to cut the cake twice in each dimension (i.e. your cut is a hyperplane orthogonal to some particular dimension). If you allow yourself to reassemble the pieces after each cut, what are the fewest number of cuts needed?
At this point, if you’re a little confused by this problem, don’t worry. Keep reading and it should get clearer.
This puzzle was inspired by Martin Gardner’s Cutting the Cube puzzle which goes as follows.
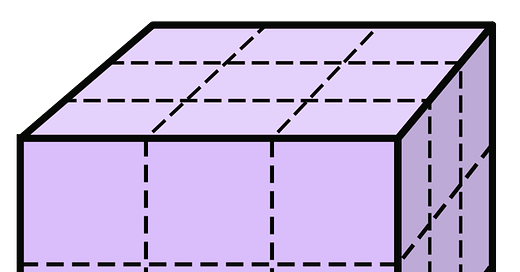
A carpenter, working with a buzz saw, wishes to cut a wooden cube, three inches on a side, into 27 one-inch cubes. He can do this job easily by making six cuts through the cube, keeping the pieces together in the cube shape. Can he reduce the number of necessary cuts by rearranging the pieces after each cut? Either show how or prove that it’s impossible.
I won’t spoil the answer to this because its a fun puzzle and it can be used to help with the solution of our hyperdimensional version of the problem. As an additional intermediate problem, I suggest extending the problem to consider a cube with 4 inch sides and 9 cuts.
To summarize, the questions this week in order are:
What is the fewest number of cuts needed to divide a cube of side length three into 27 cubes of side length 1, assuming you can rearrange the pieces of the cube as you make cuts?
What is the fewest number of cuts needed to divide a cube of side length four into 64 cubes of side length 1, assuming you can rearrange the pieces of the cube as you make cuts?
What is the fewest number of cuts needed to divide an 10-dimensional hypercube of side length 3 into 59,049 hypercubes of side length 1, assuming you can rearrange the pieces of the cube as you make cuts?
Good luck solving!
Please submit your answers here.