Our problem from 11/3/24 was
How many unique 2D shapes can be created if we ‘unfold’ the faces of the cube into one continuous piece.
How many for a dodecahedron?
An icosahedron?
This was admittedly a pretty challenging problem unless you did it by hand. For anyone that has been exposed to abstract algebra, the inclusion of platonic solids and asking for the number of “unique” shapes should have been a pretty strong clue that some group theory would be needed for this problem and that certainly is the case. If we recall back one of the canonical results of group theory—the orbit-stabilizer theorem and the closely related Burnside’s Lemma—we can recognize that we can count the number of “fixed points” for each symmetry preserving rotation and reflection action g in G.
|Orbits| in this represents the number of distinct nets, |G| is the number or rotational and reflectional symmetries of the cube (48), and |Fix(g)| is the number of different unfoldings that result in the same ultimate net for a given symmetry action g. If this is all a bit obtuse, I apologize. There isn’t really space here for me to go into sufficient detail to explain all of this so I’ll simply recommend introducing yourself to group theory.
Picking back up, we find that we have a formula that will yield the answer we want. Great! Should be easy from here. Not quite. First, we need a way to generate all possible unfoldings of the cube (remember, we aren’t yet concerned with whether these unfoldings are ‘distinct’ yet). This by itself is a bit tricky but if we think about our shape as a graph it becomes a bit more straightforward. More specifically, I think it’s easiest to model our cube as a graph where each node is a face and an edge exists between two nodes if those faces are connected on the cube. From here we can recognize that an unfolding occurs when we cut some of these edges. After cutting edges, we need to ensure there are no cycles (otherwise the shape wouldn’t be able to unfold properly) and that every node is still visited. This requires that we have exactly n-1 edges (if there were any more, we would have a cycle). There is a name for this kind of graph—namely a spanning tree—and there are a number of good algorithms for counting/generating them. For the cube there are 384.
So what we need to do is determine, for each symmetry action g in G, which of these spanning trees stays fixed under that action. We can then sum all of these values and divide by 48 to get our answer. And this is where I currently am at with this problem so far. I’m still working on how to compute the number of fixed spanning trees for each action. Of course, the answer to the questions in the puzzle can be found easily with a google search, which means you can easily back-calculate the sum of fixed points, but that’s not really the point of these puzzles! I’ll update this solution once I’ve figured out a way compute the number of fixed points under and action. And hopefully it won’t require checking each tree under each action since the number of spanning trees increases exponentially with the size of the graph so such an approach won’t work for the larger dodecahedron and icosahedron.
As always, thanks for reading! Keep an eye out for an update to this solution once I’ve finished it!
UPDATE
In my initial attempt to solve this problem, I attempted to:
Generate all spanning trees of the cube/icosahedron graph
Remove the spanning tree edges.
Use a graph hashing technique to record each of the different graphs generated. each unique hash that’s encountered represents a distinct unfolding.
At first this seemed promising but I found it didn’t yield the correct answer. After puzzling over it for a while I figured out why. Can you spot the issue?
The reason, I realized, is that the graph information doesn’t retain all the geometric information needed for this problem.
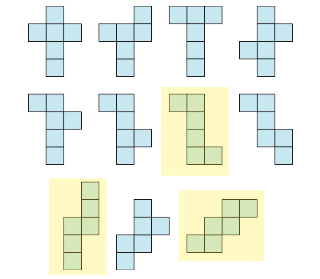
Consider what the graph of each of the highlighted unfoldings would look like. You’ll find that they would all just look like this.
So with that method out the window, what else can we do? After getting a bit stuck, I decided to consult the literature a bit and came across some very helpful papers, namely a paper from Horiyama and Shoji that provides a proof that the computation of |Fix(g)| for any convex polytope (of which the platonic solids are a subset) can be computed with—essentially—the two rules below:
Let Fix g = ∅ and all vertices not in V (Fix g) have orbits of the same length.
Then, |Fix(g) | = |T (Fix g)| · |T (Q(Γ, g))|.
Let g be of order 2 with Fix g = ∅. Then, |Fix(g)| = |T (Q(Γ, g))| · α(g).
Where Q is the quotient graph of a graph Γ over action g (vertices and edges are grouped together based on whether they are in the same orbit) and α is the number of invariant edges after the action g is applied.
From here we can use this theorem and a little help from SageMath and NetworkX to construct the symmetry group (to be specific, permutations on the vertices of the solid) and graph representation of the platonic solid. We can then compute each of the quantities detailed in the rules above. Here is some code to illustrate! Most of the values that need to be computed are reasonably clear but to help demonstrate the quotient graphs, the notebook includes visualizations of the multigraph for each action g.
And ultimately we get our solutions. For the cube there are 11 different unfoldings (which happen to be shown above) and for the icosahedron and dodecahedron (which are duals of each other so they are combinatorially the same and have the same number of unfoldings) we get 42280.
And that’s kinda all there is to it! The problem (and code) took a while to get right and there is a bit of preliminary knowledge needed to understand the rules provided by the Horiyama paper but if you’re willing to dig into those details, the rest is *reasonably* straightforward!
I know this one was pretty difficult but I hope some folks were willing to try it out and had fun with it! I very much enjoyed brushing up on some of my group theory concepts and being introduced to multigraphs, which seem like a very interesting and useful concept.