Hey everyone, apologies about the lapse in posts and this delayed solution. I would say that life got busy—which is kind of true—but the reality is I was a bit of a bum and I don’t like using busyness as an excuse. More accurately, I simply wasn’t prioritizing this as much as I should have been. I’m going to aim to be more consistent for you sake as well as mine.
If you can remember back all the way to last year, I posted this problem from 11/17/24.
Imagine you have 6 square Magna tiles. These tiles have magnets on the side so that edges of shapes will stick together. Let’s assume for a moment that toss these six square tiles onto the ground and they will land in a random configuration such that they all six are connected edge-to-edge in one large piece. What’s the probability that this configuration will be foldable into a cube without rearranging the squares?
After beginning to work on the problem, I realized there’s some ambiguities that I should have addressed. First, the resulting free hexominos aren’t all equally likely. In my opinion, that would make this problem a little bit too simple :) Instead, better description of the problem would have been
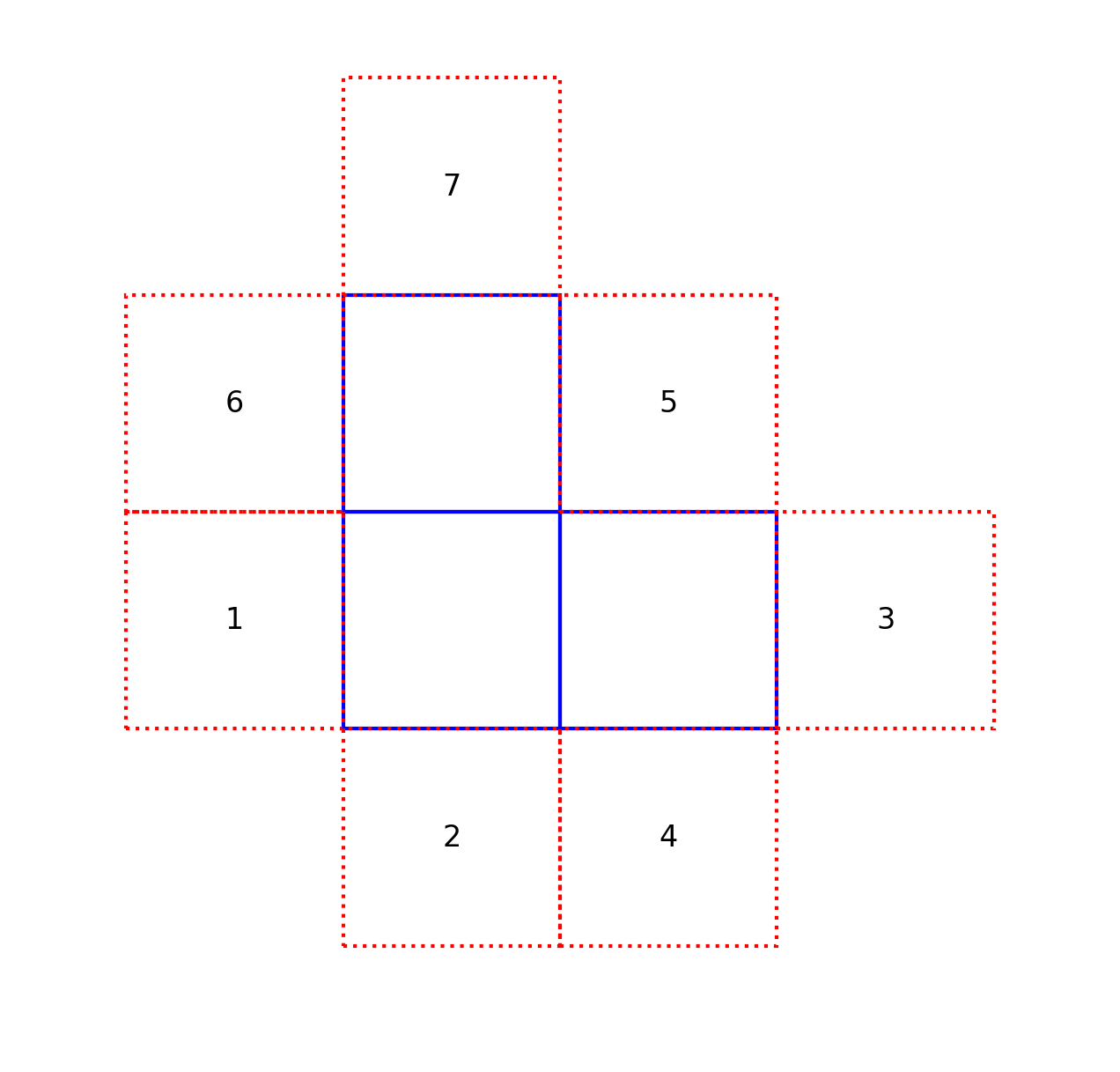
Manga tiles are dropped one by one where each tile (except for the first) is guaranteed to attach itself to the existing cluster of attached tiles. It will end up in any of the cluster’s boundary locations with equal probability. To help illustrate, the figure below shows one possible situation after 3 tiles have already been dropped. If our cluster consists of the blue squares, the fourth tile to be dropped will end up in any of locations 1-7 with equal probability.
Under this hexomino generating process, what’s the likelihood that you end up with a hexomino that can be folded into a cube?
With this clarified question in mind, we have what we need to get started.
When I was writing up this problem, I had sort of assumed that there was some semi-efficient way of generating valid polyominoes but turns out I’m wrong! Good thing I asked for the hexominos that can fold into a cube and not an equivalent question for polyiamonds and folding them into an icosahedron.
I also thought there would be a more mathy way to approach the problem but it turns out that—for the most part—solving this problem is more of a programming challenge; at least the way I solved it. My solution is posted here.
My basic approach was create a class that could iteratively construct polyominos one square at a time. The class also included the ability to generate the various symmetries of the polyomino, of which there are 8—4 rotational and 4 reflectional,1 and to test whether two polyominoes were isometric (i.e. they are the same after accounting for rotational and reflectional symmetries). With this, I could implement a simple loop that generates all the unique polyominoes of size n until we get to n=6.
Start with base monomino with count 1.
Create a new Polyomino (new_poly) by adding a square at a boundary location of (old_poly).
Check if the new Polyomino is isometric (i.e., structurally identical) to any existing Polyomino you’ve generated.
If an isometric Polyomino is found, increment its count by the count of old_poly.
If no isometric Polyomino is found, add the new Polyomino to the set with the count of old_poly.
This approach was important since it allowed me to count the number of ways of arriving at a particular polyomino shape. By maintaining this count, the probability of any given polyomino shape could be computed easily at the end by dividing a given hexomino’s count by the total count over all valid hexominoes.
Running this algorithm, we arrive at an answer of 3968/14560 or about 27.3%. This was somewhat verified by a simulation (though the number of trials was rather low given that my code ended up being pretty inefficient :/ ).
Feel free to comment with any thoughts of feedback you had on this problem or if you approached it differently. As always, thanks for reading!
