Time to cut your n-dimensional cake [Solution]
Solution for the week of 9/22/24
Our problem from 9/22/24 was
What is the fewest number of cuts needed to divide a cube of side length three into 27 cubes of side length 1, assuming you can rearrange the pieces of the cube as you make cuts?
What is the fewest number of cuts needed to divide a cube of side length four into 64 cubes of side length 1, assuming you can rearrange the pieces of the cube as you make cuts?
What is the fewest number of cuts needed to divide an 10-dimensional hypercube of side length 3 into 59,049 hypercubes of side length 1, assuming you can rearrange the pieces of the cube as you make cuts?
This puzzle ended up being a bit more am algorithms questions than a math one—at least the way I did it. If we consider the cube as a tuple of length n filled with the value L where n is the number of dimensions and L is the length of each side, then our task is to find the fewest number of cuts need to get every tuple to be filled with 1s. On each round we can cut the tuples from the previous round by taking a tuple and splitting into two tuples where all of the dimension are kept the same except one. For the dimension that’s changed, the value of that dimension in the resulting tuples need to sum the the value of that dimension in the originating tuple. In this way, we can represent a cut.
Now how can we cut optimally?
My assumption was that the optimal way to cut was to expose as many of the unexposed faces as possible. Lets first start with the three dimensional case for intuition. We have a 3x3x3 cube with 9*6=54 faces exposed and we want 27 1x1x1 cubes with 27*6=162 faces exposed. The faster we can expose these faces, the faster we’ll be done. Since “rearranging” essentially allows us to cut any resulting piece along any plane, we don’t need to consider path dependence as long as each cut is locally optimal. I included some code in my solution that verifies this for a handful of values of n and L. So what is the optimal cut, if we think in terms of exposing the most faces, the optimal cut will occur when we cut along the plane that has the highest intersectional cross-section. In terms of the tuple I described before, the cut should be along the dimension for which the product of all the other dimension is hight (assuming the dimension in question is has L=1 in which case it can’t be split any more). If we think about this as generating a binary tree, all we need to do is recursively split and keep track of which splitting path ends up being the longest.
With our tuple formulation, we can easily extend this to n-dimensions. For n=10 and L=3, we need 59,049 hypercubes each with 20 9-cube-faces. We recursively split the original hypercube with hyperplanes according to the same method talked about above and get an answer of 20. By the way, the answer to both the first two problems is 6.
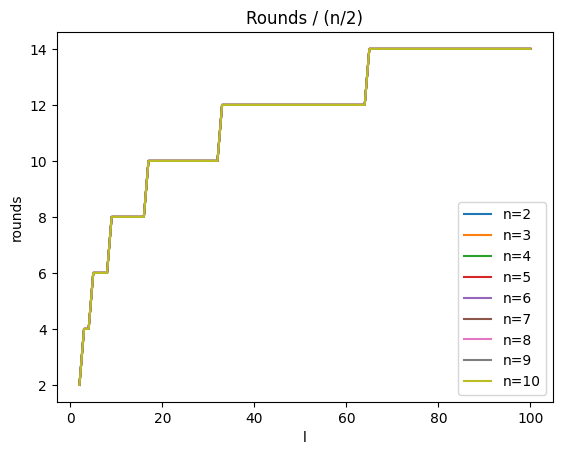
Also, if we plot the solution for different values of n and L, we’ll notice some interesting patterns.
If we scale the solutions by a factor of 2/n, they all have the same answer.
I’m still doing some analysis to figure out exactly why this is the case and why each n experiences a jump at the same value of L across all values of L. When I get some results, I’ll update the solution!
I hope you found this problem fun! As always, feel free to leave comments, thoughts, etc in the comments. Also, feel free to DM with any ideas you have for a puzzle! Hope to see you for the next one!